题目来自: leetcode 118. 杨辉三角
题目描述
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
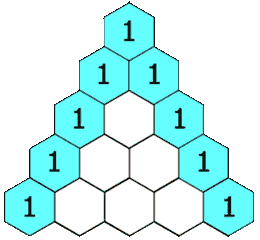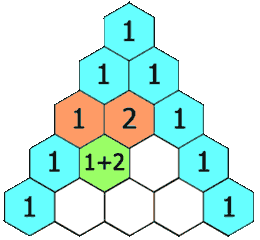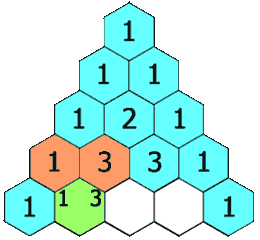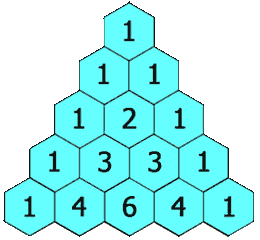
在杨辉三角中,每个数是它左上方和右上方的数的和。
示例
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
分析
百科对 杨辉三角形 的解释, 用直白一点公式就是:
triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j]
根据这个公式,就可以很容易的计算出结果, 注意下下标越界就可以了,因为 i-1 行会比 i 行少一列, 所以注意下左侧的 0 越界和右侧的 length 。
解法 1
这个是我第一时间想出来的写法, 不太优雅, 不过可以很容易表述出公式
func generate(numRows int) [][]int {
// 初始化返回的 slice
res := make([][]int,numRows)
// 如果传入的是 0 就返回个空的 slice , 如果不反悔,下面手动添加第一行数据的时候就 painc
if numRows == 0 {
return res
}
// 手动添加第一行的数据
res[0] = []int{1}
for i := 1; i < numRows; i++ {
// 创建二级数组, 长度永远比上一个长一个,因为 i 是索引, 所以 +1
sub := make([]int, i+1)
for j := 0; j < i+1; j++ {
// 获取左上的值, 给一个默认的 0, 越界的时候它就是 0, 不越界去上一行去取值
left := 0
if j > 0 {
left = res[i-1][j-1]
}
// 获取右上的值,给一个默认的 0, 越界的时候它就是 0, 不越界去上一行去取值
right := 0
if j < i {
right = res[i-1][j]
}
sub[j] = left + right
}
// 直接将新获取到的节点添加
res[i] = sub
}
return res
}
解法 2
这个和解法 1 没有本质区别, 只是代码稍微整齐了一点
func generate(numRows int) [][]int {
res := make([][]int,numRows)
var val int
for i := 0; i < numRows; i++ {
if i == 0 {
res[i] = []int{1}
continue
}
sub := make([]int, i+1)
for j := 0; j < i+1; j++ {
if j == 0 || j == i {
val = 1
} else {
val = res[i-1][j-1] + res[i-1][j]
}
sub[j] = val
}
res[i] = sub
}
return res
}
杨辉三角 II
题目来自: 杨辉三角 II
II 题目描述
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。

在杨辉三角中,每个数是它左上方和右上方的数的和。
II 示例
输入: 3
输出: [1,3,3,1]
进阶
你可以优化你的算法到 O(k) 空间复杂度吗?
II 分析
这个其实要比 I 简单, 因为永远只组要记录最后一行的值即可, 只需要注意, 它的第 k 行是 k+1 行, 如程序的 第 0 行, 对应的是图中(题目要求的) 第一行。
II 解法
这个是将每行数据从右向左添加,详细见注释, 因为 Go 向前面插入元素没那么方便,
所以从 右向左 比 左向右 要方便一些。
func getRow(rowIndex int) []int {
// 这个比三角 I 要简单, 只需要处理每行即可
// 按照题意, 第 k 行对应的是图中的 k+1 行的数据,所以及时参数是 0 ,也会有第一行的数据
res := make([]int, 1, rowIndex+1)
// 直接将第 1 行的元素定义成 1
res[0] = 1
// 因为第一行的数据已经在上面定义了, 所以只需要循环 i < rowIndex 次即可
for i:=0; i < rowIndex; i++ {
// 每次循环都将最后一个元素 1 添加
res = append(res, 1)
// 因为最后一个元素已经添加,所有从 j - 2 开始, 右向左添加
for j:= len(res) - 2; j > 0; j-- {
// 因为杨辉三角的公式,如图中, j 元素 = 上一行的 j + (j -1)元素的和
res[j] += res[j-1]
}
}
return res
}